試作人基礎講座

本日は製造業では基本となる幾何公差について解説していきます！
少し長くなるかもしれませんが、最後までお付き合いください♪

幾何公差とは

幾何公差とは、部品の形状や位置関係に関する許容誤差を定めるための規格です。
機械加工などの製造現場では、設計図面に記載された寸法や形状を忠実に再現することが求められますが、実際にはどんなに精密な加工でも多少のズレが発生します。
その「ズレ」をどこまで許容できるのかを明確にするのが、幾何公差の役割です。

たとえば、部品の穴が「直径10mmで中心がぴったり真ん中にある」ことを求めた場合、現実の加工では穴の中心がわずかにずれることがあります。
このズレを考慮し、「中心位置は±0.1mmの範囲内であれば許容する」といった基準を設けるのが幾何公差です。
寸法公差では長さや直径といった数値的な大きさの誤差を定義しますが、幾何公差は形や位置、姿勢など「幾何学的な性質」に焦点を当てています。

幾何公差には大きく分けて4つのカテゴリがあります。
形状公差（真直度や円筒度など）、姿勢公差（平行度や傾斜度など）、位置公差（位置度や対称度など）、振れ公差（円振れや全振れなど）です。
これらの項目は、設計者が意図する機能や精度に応じて図面上に記載され、製造現場や検査工程での品質基準になります。
幾何公差を明確に指定することで、必要な機能を確保しつつ、過剰な精度要求を避けて製造コストを最適化することが可能になります。
例えば、軸と穴のはめあい精度を適切に定義することで、部品の組立性や性能を向上させる一方で、必要以上に高精度な加工を避けることもできます。
また、幾何公差は国際規格（ISO）や日本工業規格（JIS）に基づいており、グローバルな設計・製造にも対応できます。
特に、複雑な機械装置や精密機器では幾何公差の適切な運用が不可欠です。
製造業における品質管理や製品信頼性の向上に直結するため、設計者や製造担当者はその意味と使い方を正確に理解する必要があります。

寸法公差との違い

幾何公差とよく混同されがちな概念に「寸法公差」があります。
どちらも「公差」という言葉を含み、製造物のばらつきを制限するための規格ですが、その役割と適用範囲には明確な違いがあります。
この違いを理解することで、設計者はより適切に製品の要求精度を伝えることができ、製造や検査工程における無駄やミスを防ぐことができます。

寸法公差とは、部品の「サイズ」に対する許容範囲を指します。
たとえば「直径10mm ±0.1mm」という指定は、穴や軸の太さが9.9mmから10.1mmの間であれば合格とするという意味です。
このように、寸法公差は長さ、幅、直径などの数値的な大きさに対して適用されます。
対象はあくまで「寸法（サイズ）」であり、形や位置、向きまでは考慮していません。
一方、幾何公差は「形状」や「位置関係」に焦点を当てた公差です。
たとえば、ある面がどれだけ真っ直ぐであるべきか（真直度）、ある軸が基準面に対してどれだけ直角であるべきか（直角度）、ある穴の中心がどこに位置しているべきか（位置度）といった、寸法以外の幾何学的要素を制御します。
これにより、部品の機能性をより厳密に保証できるのです。
また、寸法公差だけでは制御できない精度項目も多く存在します。
たとえば、直径は規定どおりでも穴の中心位置がずれていれば、部品同士が正しく組み合わない可能性があります。
このようなケースでは、幾何公差によって位置や姿勢を明確に指定する必要があります。
つまり、寸法公差は「大きさの制限」、幾何公差は「形状や位置の制限」という役割分担があります。

両者は併用されることが一般的であり、それぞれの特性を理解して適切に使い分けることが求められます。
過剰に寸法公差だけで精度を追求すると、製造コストが不必要に高騰してしまうこともあります。
逆に幾何公差を活用すれば、機能に必要な箇所だけを高精度に管理し、他は許容範囲を広く取ることでコストを抑えつつ品質を維持することができます。
まとめると、寸法公差は「数値的な大きさの誤差」を管理し、幾何公差は「形状や位置・姿勢の誤差」を管理するものであり、それぞれの得意分野に応じて設計図面上で明確に使い分けることが、製品の機能性と生産性を両立させる鍵となります。

幾何公差が重要な理由

幾何公差は、製品の品質・信頼性・機能性を保証する上で極めて重要な役割を果たします。
寸法公差のみでは制御しきれない形状や位置のばらつきを管理できるため、特に高精度が要求される製品や複雑な組立工程を伴う製品において、幾何公差の有無が完成品の性能や不良率に大きく影響します。
たとえば、機械装置に使われるシャフトと軸受の関係を考えてみましょう。
シャフトが寸法的には正しく加工されていても、中心がずれていたり、軸の向きが傾いていたりすれば、正しく回転せず摩擦が増えたり、最悪の場合は破損につながります。
ここで幾何公差を活用することで、真直度、同心度、直角度といった項目ごとに許容されるズレの範囲を明確に設定し、実用上問題のない部品の基準を統一できます。

さらに、幾何公差を適切に設定することで、製品の組立性の向上にもつながります。
多くの製品は複数の部品で構成されており、それぞれが決められた位置や角度で組み合わされることで機能を果たします。
部品ごとのズレが大きいと、組立作業での調整が難しくなったり、ガタや干渉が発生したりします。
幾何公差を用いることで、そうしたズレを管理し、スムーズな組立を実現できます。
また、製造コストと品質のバランスを取るためにも幾何公差は有効です。
寸法公差だけで形状を厳しく管理しようとすると、すべての加工精度を必要以上に高く保たなければならず、結果的にコストが膨らんでしまいます。
対して、幾何公差を使えば、製品の機能に影響のある箇所にのみ精度を集中させ、それ以外の箇所にはゆるやかな基準を設けることで、必要最小限のコストで必要十分な品質を得ることが可能になります。
さらに、グローバル化が進む中で、国際規格（ISO）に準拠した設計・製造の基盤としても幾何公差は欠かせません。
海外企業との取引や製品輸出の場面では、共通のルールとして幾何公差が使用されており、適切な指定がなければ図面の意図が伝わらず、誤解による不具合や手戻りが発生するリスクもあります。
幾何公差の明確な運用は、設計意図を正しく伝える「言語」としての役割も担っているのです。
このように、幾何公差は単なる「精度の管理手法」ではなく、製品の品質保証、コスト削減、作業効率、国際対応といった複数の観点から極めて重要な要素となっています。
設計者・製造者・検査者の全てがその重要性を理解し、正しく活用することが製造現場における競争力強化に直結すると言えるでしょう。

形状公差

引用元：アイアール技術者教育研究所 【機械製図道場・上級編】幾何公差の図示を習得！幾何公差の種類・特性・記号は？データムって何？

形状公差は、個々の要素（面や線など）が理想の形状からどの程度ずれていても許されるかを規定するものです。
これらは他の要素との関係を必要とせず、単独の形状そのものに対して適用されます。
幾何公差の中でも基本的かつ重要なカテゴリであり、真直度・平面度・真円度・円筒度の4つが代表的です。

真直度

真直度は、直線として理想的に存在すべきエッジや軸が、どれだけ曲がっていても許されるかを定める公差です。
たとえば、長いシャフトがわずかにたわんでいる場合、そのたわみが公差内であれば「真直度良好」と判断されます。
公差値が小さいほど、よりまっすぐである必要があります。
真直度の制御は、回転体の芯ぶれや直線運動部の滑らかさに直結するため、非常に重要です。

平面度

平面度は、面がどれだけ平らであるか、つまり凹凸やうねりの許容範囲を定めます。
たとえば、機械部品の接触面やシール面が凹んでいたり波打っていたりすると、漏れや隙間が生じてしまいます。
平面度の管理は、部品同士の密着性、剛性、安定性に大きく関わります。
特に金型部品や精密機器の接触面では、厳しい平面度が求められます。

真円度

真円度は、円として理想的であるべき断面が、どれだけ真円からずれていても許されるかを示します。
真円度が悪いと、例えば回転する軸やベアリングの動作が不安定になり、摩耗や振動の原因になります。
真円度の測定には、真円度測定機や表面粗さ測定器を使うことが一般的です。

円筒度

円筒度は、真円度・真直度・平面度を複合した概念で、円筒全体がどれだけ理想的な円筒形状をしているかを評価するものです。
たとえば、長い軸の外周面がゆがんでいたり、テーパーがついていたりすると、ベアリングとの嵌合精度に問題が生じます。
円筒度は高精度な回転軸、ピストン、スリーブなどの部品で重要視されます。

形状公差の活用メリット

形状公差を適切に設定することで、製品の性能安定性や寿命を大きく向上させることができます。
たとえば、精密に加工された真直なガイドレールは、摩耗が少なく安定した動作を長期間保つことができます。
一方で、不要に厳しい形状公差を指定してしまうと、加工難易度が上がり、コストや歩留まりに悪影響を及ぼすこともあります。
したがって、どの程度の精度が本当に必要なのかを見極めた上での設計が重要です。

姿勢公差

引用元：アイアール技術者教育研究所 【機械製図道場・上級編】幾何公差の図示を習得！幾何公差の種類・特性・記号は？データムって何？

姿勢公差とは、ある幾何要素（面や線など）が、他の基準となる要素に対してどのような姿勢（方向・角度）で存在すべきかを規定する公差です。
形状公差が「単独の形」に対する精度を定めるのに対して、姿勢公差は「相対的な角度や方向性」に着目するのが特徴です。
製品の組立精度や機能性を確保するためには、部品同士が正しい角度関係で組み合わさる必要があります。
そのため、姿勢公差は非常に実用的かつ重要な要素となります。
代表的なものに「平行度」「直角度」「傾斜度」があります。

平行度

平行度は、ある面や線が、基準となる面や線に対して、どれだけ平行であるべきかを定める公差です。
たとえば、スライド機構やレール、ガイド部など、相対運動を行う構造では平行性の確保が重要になります。
わずかな角度ずれでも、動作不良や摩耗の原因となるため、正確な平行度管理が不可欠です。
平行度の公差は、対象となる幾何要素が「ある基準面からどれだけ離れていてもよいか」という幅として表現されます。
たとえば、0.01mmの平行度公差がある場合、指定された面は基準面に対して±0.005mm以内のずれに収まっていなければなりません。

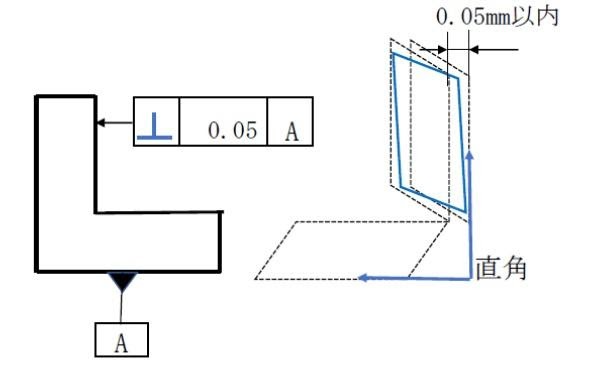
直角度

直角度は、ある面または線が、基準面または基準線に対してどれだけ正確に直角（90度）であるかを規定する公差です。
例えば、ネジ穴が基準面に対して傾いていると、部品の締結力が不安定になり、製品の強度や密閉性が損なわれる恐れがあります。
特に、箱型部品やハウジングの角部、機構部の軸と壁面の関係など、直交関係が求められる場面では直角度の指定が不可欠です。
測定には三次元測定機や角度測定機器が用いられます。

傾斜度

傾斜度は、基準要素に対して指定された角度（たとえば30度や45度など）を保つべき幾何要素の、角度の誤差を管理する公差です。
これは、平行度や直角度と似ていますが、「任意の角度」を対象とする点が特徴です。
たとえば、部品に対して斜めに設けられた面や溝、テーパー部などは、角度がずれることで機能性に大きな影響が出ます。
傾斜度公差を指定することで、製品の斜角部分の精度が保証され、組立や動作における不具合を未然に防ぐことができます。

線の輪郭度

線の輪郭度は、部品の特定の断面の輪郭形状が、理想的な形状（理論輪郭）からどれだけ離れてよいかを定める公差です。
曲線や斜面、滑らかな形状など、通常の寸法公差では表現しづらい複雑な輪郭に対して使われます。
たとえば、自動車のエンジン部品のようにエアフローに影響する形状や、流線形の外装部品などでは、断面ごとの滑らかさが求められます。
このとき線の輪郭度を使えば、「理想曲線に±0.1mm以内で形状が一致していること」を明確に規定できます。
測定にはプロファイル測定器や3Dスキャナ、三次元測定機などが用いられ、断面形状をスキャンし、理論輪郭と実測輪郭の差分を算出して評価します。

面の輪郭度

面の輪郭度は、部品の三次元的な表面全体の形状が、理想的な面からどれだけずれてよいかを示す幾何公差です。
線の輪郭度の三次元版と考えることができます。
自由曲面や空力形状、光学レンズ、医療用インプラントなど、極めて精密で複雑な形状が求められる部品では、面全体の滑らかさ・整合性が必要です。
面の輪郭度を使えば、「設計通りの滑らかな曲面になっているか」を数値で保証できます。
この公差も非常に高精度な測定が必要なため、非接触式三次元スキャナや干渉計、接触式プローブなどを用いて、実測面と理論面の誤差をマッピングします。

姿勢公差の活用と注意点

姿勢公差を適切に設けることで、部品の角度的な関係性を保証でき、精密な組立・摩耗低減・性能安定化が実現します。
たとえば、基板を装着するフレームに対して、端子が正確に直角で取り付けられていなければ、接続不良を起こす可能性があります。
こうした問題を避けるために、姿勢公差は設計段階での必須要素と言えます。
ただし、姿勢公差は基準要素の設定が前提となるため、図面上では必ず基準を明示する必要があります。
また、過剰に厳しい公差を設定してしまうと加工や測定のコストが高騰してしまうため、「製品の機能に必要な最小限の公差」にとどめることが設計のポイントです。

位置公差

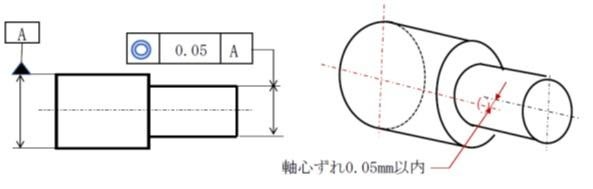
引用元：アイアール技術者教育研究所 【機械製図道場・上級編】幾何公差の図示を習得！幾何公差の種類・特性・記号は？データムって何？

位置公差とは、ある幾何要素（穴や軸、面など）が、図面で定義された理想的な位置に対してどの程度ずれても良いかを示す公差です。
特に複数部品の組み立てや、相手部品との嵌合精度が必要な部分において重要です。
正しい寸法で加工されたように見える部品でも、わずかな位置のズレがあるだけで、穴が合わなかったり、シャフトが偏芯していたりといった不具合が発生することがあります。
これを防ぐのが位置公差の役割です。
代表的なものとして「位置度」「同心度」「対称度」があります。

位置度

位置度は、ある幾何要素（例えば穴の中心やボスの軸など）が、基準からの理想的な位置に対してどれだけずれても許されるかを示す公差です。
一般的に、XY座標で指定された理論的な位置からの「半径方向のずれの範囲」で表現されます。
たとえば、部品に4つの取付け穴がある場合、穴の位置がずれていると、ボルトが入らなかったり、他の部品との組立ができなくなります。
位置度を指定することで、穴位置の精度を厳しく管理し、スムーズな組立や機能の確保が可能になります。
位置度の測定には、三次元測定機（CMM）や、特定の基準治具を使うことが一般的です。

同心度

同心度は、軸や円筒形状の中心が、基準となる他の軸に対してどの程度一致しているかを定める公差です。
たとえば、シャフトとその外周に取り付けられたギアが、それぞれの中心軸からずれていた場合、回転時にぶれが発生し、異音や摩耗の原因になります。
同心度公差では、2つの要素の中心軸が「1つの共通軸上にある」ことを保証します。
加工工程では芯出し精度が重要となり、測定にも精密な機器が必要です。
近年では、同心度の代わりに位置度を使って管理するケースも増えています。
なぜなら、同心度は測定難易度が高く、コストや工数がかさむからです。

同軸度

同軸度とは、ある軸が、別の基準軸と同じ中心軸上に存在しているかどうかを示す幾何公差です。
回転体や円筒形状の部品において、複数の軸が真っすぐにそろっていないと、組み立て時にがたつきや摩耗の原因になります。
同心度と似ていますが、同軸度は軸（中心線）自体の直進性や方向も評価の対象になる点が特徴です。
例えば、シャフトの両端や途中に段付き形状がある場合、各段がバラバラの軸方向を向いていると振動や騒音の原因になります。
そこで、1本の基準軸を指定し、それに対して他の軸がどれだけ同軸であるかを指定することで、製品の回転精度や組立て精度を確保します。
測定にはCNC三次元測定機が用いられることが多く、基準軸に対して対象軸のずれ量（中心線の偏差）を評価します。
同軸度の厳格な管理は、ベアリングやモーター部品、光学装置など、高精度な回転・位置制御が求められる機器で必須です。

対称度

対称度は、ある幾何要素が、指定された基準面や軸に対して、どれだけ対称であるかを管理する公差です。
対象物の左右または上下がきちんと対称でなければ、見た目の不良や組み立て不良につながる恐れがあります。
たとえば、金属のカバーや装飾部品など、対称性が求められる部品では、対称度が重要です。
また、光学部品やセンサー部品のように対称性が機能に直結する部品でも欠かせません。
対称度も同心度と同様、測定がやや難しいため、実務上では位置度で代用される場合が多くなっています。

位置公差のポイントと活用法

位置公差は、「図面通りの組立て精度」を保証する手段として設計・製造において非常に重要です。
特に近年は自動化やロボット組立が主流になり、人の手による微調整が効かない現場も多いため、設計段階での正確な位置公差設定が必要不可欠です。
ただし、必要以上に厳しい公差は加工費を高騰させる要因にもなるため、「どの機能を保証したいのか」「そのためにどこにどの程度の精度が必要なのか」を明確にすることが重要です。
また、測定性も考慮し、現場で無理なく確認できる基準や方法を設けることもポイントです。

振れ公差

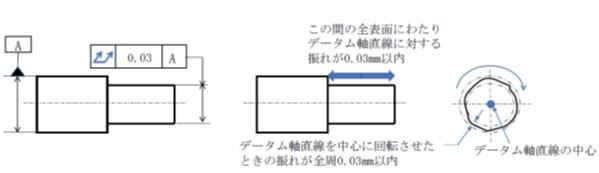
引用元：アイアール技術者教育研究所 【機械製図道場・上級編】幾何公差の図示を習得！幾何公差の種類・特性・記号は？データムって何？

振れ公差とは、回転する部品や円筒形状の部品に対して、その回転軸や回転面がどれだけ理想的な運動からずれていないかを評価するための公差です。
主に「円振れ」と「全振れ」の2種類があり、これらは部品の回転精度や真円度に大きな影響を与える重要な公差です。
たとえば、シャフトや軸受、ディスクなど、回転を伴う部品では、振れが大きいと「異音」「振動」「偏摩耗」などのトラブルを引き起こす恐れがあります。
そのため、振れ公差によって回転中心との偏差を制限することが必要です。

円振れ

円振れは、回転軸に対して、ある断面における表面がどれだけ「ブレ」ているかを示す公差です。
部品を360度回転させた際、特定の位置での変位（振れ）量の最大値と最小値の差が公差値を超えてはいけません。
具体的には、ダイヤルゲージを当てて測定し、ある断面において最大と最小の読み取り値の差が「円振れ公差」になります。
たとえば0.02mmの円振れ公差が指定されている場合、360度回転させた際のダイヤルゲージの振れ幅が0.02mm以内でなければならないということです。
円振れは、軸受部や回転体の端部など、1つの断面だけで評価される点が特徴です。

全振れ

全振れは、ある軸または面に対して、その全体の真直度や真円度を総合的に評価する公差です。
円振れとは異なり、全振れでは「全長」または「全面」で測定を行い、軸方向に沿って回転させた際の全範囲の振れ量をチェックします。
たとえばシャフトの軸全体のブレや、フランジ面全体の傾きや歪みなど、広範囲にわたる精度が求められる部品では、円振れではなく全振れが使用されます。
これにより、表面全体が均一に回転していることが保証されます。
測定方法としては、被測定物を回転させながら、長手方向または面方向にダイヤルゲージを滑らせ、振れ幅を記録します。
回転運動の中での「全体的なブレ」を見たい場合に非常に有効です。

振れ公差の重要性と実務上の考え方

振れ公差は、単なる「位置や姿勢」ではなく、実際の動作における挙動を規制するものであるため、特に回転部品における機能性と耐久性に直結します。
たとえば、モーターシャフト、ベアリング部、ディスク、プーリーなどで振れが大きいと、機械全体の性能低下を招く可能性があります。
また、測定には回転治具や高精度なゲージ類が必要で、精密加工や高機能機器ではNC旋盤や研削盤による高精度加工が求められます。
実務上では、「まず円振れで管理し、それでも不十分な場合に全振れを採用する」という考え方が一般的です。
これは、全振れのほうがより厳しい管理を必要とするためです。

円振れ・全振れの使い分けポイント

区分	管理対象	測定範囲	用途例
円振れ	特定の断面	1点または1断面	軸端の精度、フランジの接触面
全振れ	全体（軸や面）	全長または全面	シャフト全体、面の歪み管理

これらの使い分けにより、適切な回転精度を確保し、製品の長寿命化・信頼性向上に寄与します。

他、ブログ記事もご覧ください♪

動画の投稿もしておりますので良ければご覧ください♪